
Listen To This Blog
Introduction
Welcome to the fascinating world of quadrilaterals, a fundamental concept in geometry that plays a pivotal role in our understanding of shapes and structures. Quadrilaterals, with their four-sided allure, are not just mere figures on a paper; they are the building blocks of much of the world around us. From the architectural marvels that define city skylines to the digital screens we gaze into daily, quadrilaterals make up an integral part of our everyday life. This guide aims to delve into the various aspects of these four-sided shapes, exploring their unique properties, diverse types, and practical applications. Whether you're a student grappling with geometric principles, a professional seeking a refresher, or simply a curious mind intrigued by the mathematical tapestry of the universe, this exploration of quadrilaterals promises to be both enlightening and engaging. Let's embark on this journey to uncover the secrets and solve the puzzles that quadrilaterals present in our fascinating geometric landscape.
The Definition of a Quadrilateral
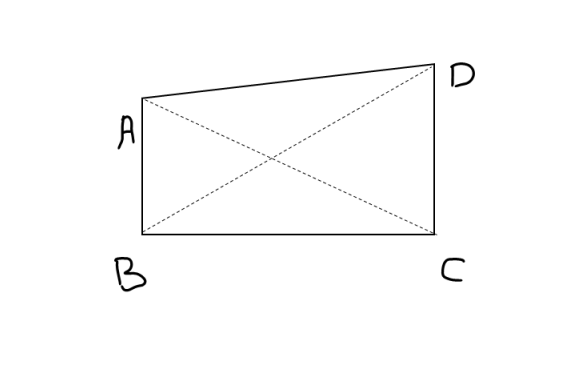
A quadrilateral stands as a cornerstone in the study of geometry, defined by its four distinct sides enclosing a single, closed shape. This geometric figure is characterized by four vertices or corners, each joining two of its sides, and four angles, each nestled at these vertices. The beauty of a quadrilateral lies in its diversity; it can manifest in various forms, from the strict symmetry of squares to the elongated elegance of rectangles, and even the dynamic shapes of kites and trapezoids. Each quadrilateral, while unique in form, shares the unifying property of having its interior angles sum up to 360 degrees, a testament to the harmony and balance inherent in geometric designs.
The Properties Of Quadrilaterals: A Closer Look
Diverse Angles and Sides
Quadrilaterals, at their core, are defined by having four sides and four angles. This fundamental trait sets the stage for a variety of shapes, each with its unique characteristics. The sum of the internal angles in any quadrilateral always adds up to 360 degrees, a key aspect that remains constant across all types.
Varied Side Lengths and Parallels
The lengths of the sides in quadrilaterals can vary greatly. Some, like squares, boast equal sides, while others, such as rectangles, have alternating longer and shorter sides. The concept of parallel sides also comes into play, with shapes like parallelograms and trapezoids showcasing this feature prominently.
Diagonal Dynamics
Diagonals in quadrilaterals offer intriguing properties. They can bisect each other, be equal in length, or intersect at specific angles, contributing to the shape's overall geometry. The behavior of diagonals is a key aspect in distinguishing between different types of quadrilaterals.
These properties not only define the basic structure of quadrilaterals but also pave the way for deeper exploration into their geometric identities and applications.
Sum of Interior Angles in Quadrilaterals: A Fresh Perspective
Understanding the sum of interior angles in quadrilaterals is a key aspect of geometry that reveals much about these four-sided figures. The concept is simple yet profound: no matter what type of quadrilateral you are dealing with, the sum of its interior angles always adds up to 360 degrees. This universal truth holds whether you're examining a classic rectangle, a dynamic kite, or any other quadrilateral form.
The Formula and Its Proof
Formula: The sum of the interior angles of a quadrilateral = 360°.
Proof:
- Constructing the Quadrilateral: Consider any quadrilateral, say ABCD. This figure has four angles, namely ∠A, ∠B, ∠C, and ∠D.
- Drawing a Diagonal: Draw a diagonal from one vertex, say from A to C. This diagonal divides the quadrilateral into two triangles, △ABC and △ACD.
- Applying the Triangle Angle Sum Property: We know that the sum of angles in a triangle is 180°. Therefore, for △ABC, the sum of angles ∠CAB, ∠ABC, and ∠BCA is 180°. Similarly, for △ACD, the sum of angles ∠CAD, ∠ACD, and ∠DCA is also 180°.
- Combining the Angles: Adding the sums of the angles of both triangles, we get:
- Sum of angles in △ABC + Sum of angles in △ACD = 180° + 180° = 360°.
- This translates to (∠CAB + ∠ABC + ∠BCA) + (∠CAD + ∠ACD + ∠DCA) = 360°.
- Rearranging the Angles: Notice that ∠CAB and ∠CAD make up ∠A, ∠ABC and ∠ACD make up ∠B, and so on. Therefore, we can rewrite the equation as: ∠A + ∠B + ∠C + ∠D = 360°.
This proof elegantly demonstrates that no matter how you shape a quadrilateral, the total measure of its interior angles will always be a constant 360 degrees. This principle is not just a mathematical curiosity; it's a fundamental aspect that underpins many practical applications in fields ranging from architecture to computer graphics. Understanding this concept opens up a world of possibilities in both theoretical and applied mathematics.
The Types of Quadrilaterals: A Diverse and Intriguing Array
Quadrilaterals, the versatile and fundamental shapes in geometry, come in various forms, each with its unique set of properties and characteristics. Understanding these types is essential for anyone delving into the world of geometry, design, or any field where these shapes play a crucial role. Let's explore the different types of quadrilaterals and focus on the parallelogram, a particularly interesting and widely applicable form.
Parallelogram: A Model of Symmetry and Balance
The parallelogram stands out with its parallel opposite sides, a feature that gives it both its name and distinctive properties. It's a shape that you often encounter in various fields, from architecture to graphic design.
Properties of a Parallelogram:
- Opposite Sides Parallel and Equal: Each side of a parallelogram is parallel to its opposite, and these opposite sides are of equal length.
- Opposite Angles Congruent: The angles facing each other across the shape are equal, lending a symmetrical look to the parallelogram.
- Consecutive Angles Supplementary: Each pair of angles along the same side adds up to 180 degrees.
- Diagonals Bisect Each Other: The diagonals of a parallelogram intersect each other, dividing each other into two equal parts.
Formulas of Parallelograms
Parallelograms are unique quadrilaterals with intriguing properties and formulas that are essential in geometry. Characterized by opposite sides that are both parallel and equal in length, parallelograms present a fascinating study in symmetry and balance. The angles on opposite corners are congruent, adding to their distinct shape.
Key Properties
- Opposite sides are parallel and equal in length.
- Opposite angles are equal.
- Consecutive angles are supplementary (add up to 180 degrees).
- Diagonals bisect each other, dividing the parallelogram into two congruent triangles.
Essential Formulas
- Area: The area of a parallelogram is calculated using the formula: Area = Base × Height (A = b × h).
- Perimeter: To find the perimeter, the formula is: Perimeter = 2(Length + Breadth) (P = 2(l + b)).
These properties and formulas not only make parallelograms a topic of interest in geometry but also lend them practical applications in various fields, from architecture to design.
Formula and Properties of Rectangles
Rectangles, a cornerstone in the world of quadrilaterals, are renowned for their simplicity and symmetry. These four-sided figures are characterized by their opposite sides being equal and parallel, and each of their four angles measuring a perfect 90 degrees. This geometric harmony lends itself to straightforward calculations and applications.
Key Properties:
- Opposite Sides Equal and Parallel: Each rectangle has its opposite sides matching in length and running parallel to each other.
- Right Angles: All four corners of a rectangle are right angles, making it an exemplar of perpendicularity.
- Congruent Diagonals: The diagonals of a rectangle are not only equal in length but also bisect each other, creating a mirror symmetry.
Formula for Area and Perimeter:
- Area: The area of a rectangle is found by multiplying its length (L) by its breadth (B), expressed as Area=L×B.
- Perimeter: To find the perimeter, add the lengths of all four sides, or simply calculate it as Perimeter=2(L+B).
These properties and formulas make rectangles a fundamental element in various fields, from architecture to design, underscoring their ubiquitous presence in our daily lives.
Formula and Properties of a Square
A square, a special kind of quadrilateral, is renowned for its equal sides and angles. Each of the four sides of a square is of the same length, and every angle is a perfect right angle, measuring 90 degrees. This symmetry and uniformity lend the square some interesting properties and a simple, yet elegant formula.
Formula for the Area of a Square:
The area is calculated as the length of a side squared, denoted as Area=L2, where L represents the length of one side.
Properties of a Square:
- Equal Sides: All four sides of a square have the same length.
- Equal Angles: Each angle in a square measures 90 degrees.
- Diagonals: The diagonals of a square are equal in length and bisect each other at right angles.
- Perimeter: The perimeter of a square, the total length around the boundary, is four times the length of a side, expressed as Perimeter=4L.
These properties make the square not only a fundamental shape in geometry but also a widely used element in various fields, from architecture to design.
Formula and Properties of a Rhombus
A rhombus, often recognized for its diamond-like shape, is a unique type of quadrilateral with intriguing properties and a simple yet elegant formula. Characterized by four equal-length sides, this geometric figure stands out for its symmetry and balance. The properties of a rhombus include congruent opposite angles and diagonals that bisect each other at right angles, creating a perfect cross at the center. This intersection of diagonals not only bisects each angle but also divides the rhombus into congruent triangles, adding to its geometric charm.
When it comes to calculating the area of a rhombus, the formula is straightforward: Area = (Diagonal 1 × Diagonal 2) / 2. This formula leverages the lengths of the diagonals, denoted as 'Diagonal 1' and 'Diagonal 2', which intersect perpendicularly. Thus, by simply knowing the lengths of these diagonals, one can easily determine the area of this equilateral quadrilateral, making it a handy tool in both academic and practical applications.
Wrapping Up
In conclusion, diving into the world of quadrilaterals reveals the richness and complexity of geometric shapes, a crucial element in math assignments. For students and enthusiasts seeking to deepen their understanding, this exploration offers invaluable insights. If you find yourself needing further assistance or guidance, GreatAssignmentHelper stands ready as a reliable assignment helper. Their expertise can provide clarity and support, ensuring a comprehensive grasp of these fundamental geometric concepts. Whether for academic success or personal enrichment, the journey through the realm of quadrilaterals is both rewarding and enlightening.

