How to Find the Median | Definition, Examples & Calculator

Introduction

In the world of statistics, grasping the concept of the median is crucial for anyone looking to analyze and interpret data effectively. This central value serves as a pivotal point, neatly dividing a dataset into two halves, ensuring a clear perspective on the distribution of values. Whether you're dealing with financial figures, test scores, or any numerical data, understanding the median enhances your analytical capabilities. It shines especially bright in scenarios where data points are skewed or contain outliers, offering a more accurate reflection of the dataset's center than other measures might. Let's dive into the essentials of finding and applying the median, equipping you with the knowledge to tackle your data with confidence.

What is Median?

The median is a statistical measure that identifies the middle value in a given set of numbers, effectively splitting the dataset into two equal parts. When the numbers are sorted in ascending or descending order, the median stands out as the central point for both evenly and oddly numbered datasets. It's particularly valuable in providing a realistic sense of the data's central tendency, especially in cases where the dataset includes outliers or is not symmetrically distributed. By focusing on the median, analysts and researchers can gain insights into the typical value, bypassing the skew that extreme values might introduce.

How to Calculate the Median

Calculating the median is a straightforward process that brings clarity to the central tendency of a dataset. Here’s how you can do it:

1. Organize Your Data: Start by arranging your data points in ascending order, from the smallest to the largest value. This step is crucial for accurately identifying the median.
2. Determine the Dataset Size: Count the number of data points in your dataset to figure out whether you have an odd or even number of values.
3. Find the Median for Odd-Sized Datasets: If your dataset has an odd number of values, the median is the value that sits right in the middle. For example, in a dataset of 7 numbers, the fourth number is the median.
4. Calculate the Median for Even-Sized Datasets: For datasets with an even number of values, the median is found by calculating the average of the two middle numbers. If you have 8 numbers, average the fourth and fifth values to get the median.

By following these steps, you can accurately determine the median, providing a clear view of the middle ground in your dataset, regardless of any outliers or skewed data.

Figuring Out the Median: A Step-by-Step Guide with Formula

Determining the median of a dataset involves a simple yet effective formula that helps pinpoint the central value. Here's how you can figure it out:

• Sort Your Data: Arrange all data points in your set in ascending order, from the smallest to the largest.
• Count Your Data Points: Identify the total number of data points in your dataset, denoted as N.
• Apply the Median Formula:
  • For an odd number of data points, the formula to find the median position is (N+1)/2. The result points to the position of the median value in the sorted list.
  • For an even number of data points, you calculate the median by averaging the values in the two middle positions, which are found using the formulas N/2 and N/2)+1.

Example for Odd-Sized Dataset: If you have 7 data points, your median position is (7+1)/2=4(7+1)/2=4. The fourth value in your sorted list is the median.

Example for Even-Sized Dataset: With 8 data points, the median is the average of the 4th and 5th values in the sorted list.

This method ensures that you accurately determine the median, offering a clear view of your dataset's central value, especially useful in skewed distributions or when outliers are present.

Finding the Median in an Odd-Numbered Dataset

When dealing with an odd-numbered dataset, finding the median is a straightforward process that allows you to identify the central value with ease. Here's how to do it:

1. Sort the Data: Begin by arranging all the data points in your set from the lowest to the highest value. This step is crucial for accurately locating the median.
2. Count the Data Points: Determine the total number of data points in your dataset. Let's denote this number as N.
3. Identify the Median Position: Since the dataset has an odd number of data points, the median will be the value that directly occupies the middle position. You can find this position by using the formula: (N+1)/2. This formula gives you the exact position of the median in your sorted list.
4. Locate the Median Value: Go to the position identified in the previous step and select the value that resides there. This value is your median.

For example, if your dataset consists of 9 values, after sorting them, the median will be at position (9+1)/2=5(9+1)/2=5. Therefore, the fifth value in your ordered list is the median.

This method ensures that you accurately capture the central tendency of your dataset, providing a clear insight into its distribution, particularly useful for skewed data or datasets with outliers.

Finding the Median in an Even-Numbered Dataset

Determining the median in a dataset with an even number of values involves a slightly different approach than with an odd-numbered set. Here's a clear, step-by-step guide to accurately find the median in such cases:

1. Sort Your Data: Begin by arranging all the values in your dataset in ascending order. This means listing the numbers from the smallest to the largest. This step is crucial for accurately identifying the median.
2. Identify the Middle Positions: In an even-numbered dataset, there isn't a single middle value but rather two middle values. Calculate the positions of these two values by finding N/2 and (N/2)+1, where N is the total number of data points in your dataset.
3. Locate the Middle Values: Once you have identified the two middle positions, locate the corresponding values in your sorted dataset. These are the two numbers that sit right in the center of your dataset.
4. Calculate the Median: The median is the average of these two middle values. Add them together and divide by 2: (vlaue ((N)⁄(2)+value(N⁄(2)+1)))/2^.  . This calculation gives you the median, providing a central value that represents the middle ground of your dataset.

This method ensures that you accurately determine the median in an even-numbered dataset, offering a fair representation of the dataset's central tendency, particularly useful for understanding distributions that may be skewed or contain outliers.  

Finding the Median with Ordinal Data

Determining the median in a dataset composed of ordinal data—where the data points are ranked in order but not necessarily equidistant from each other—follows a conceptually similar approach to that used with numerical data, albeit with a focus on the order of ranks rather than numerical values. Here's how to approach this:

• Organize the Data: Start by arranging your ordinal data in order, from the lowest to the highest rank. This could range from qualitative assessments like "poor" to "excellent" or "first" to "last."
• Count the Data Points: Determine the total number of observations in your dataset. This count will guide you in identifying the median's position.
• Identify the Median Position:
  • For datasets with an odd number of observations, the median is the value at the exact middle position after ordering the data. This is straightforward since one value will naturally occupy this central position.
  • For datasets with an even number of observations, the median is less about finding a numerical average and more about identifying the two central ranks. The median, in this case, is conceptualized as lying between these two ranks. If a precise value is needed, one might consider the categories these ranks represent and choose an appropriate method to determine a middle ground, acknowledging the limitations of averaging ordinal data.
• Locate the Median Value: Once the median position is determined, select the value or values that occupy this position. In ordinal data, the median reflects the central tendency in terms of ranking order, providing insights into the distribution of categories or ranks within your dataset.

This method of finding the median in ordinal data sets is particularly useful for understanding the central trend of non-numerical, ranked information, offering a clear view of the middle rank within the dataset. It's an invaluable tool in fields like survey research, educational assessment, and any area where qualitative rankings provide critical data insights.

Odd-Numbered Dataset: Calculating the Median

For an odd-numbered dataset, the formula to find the median is straightforward, focusing on locating the central value that divides the dataset into two equal halves. Here's the formula used to calculate the median in such datasets:

• Median Position Formula: N/2+1​

Where N is the total number of observations in the dataset.

Application:

1. Sort the Data: Ensure your data is ordered from lowest to highest.
2. Apply the Formula: Use the median position formula to find the exact middle position in your sorted dataset.
3. Identify the Median: The value at this position is the median of your dataset.

This method provides a clear and precise way to determine the central tendency of an odd-numbered dataset, offering valuable insights into the distribution of your data.

When to Use the Median

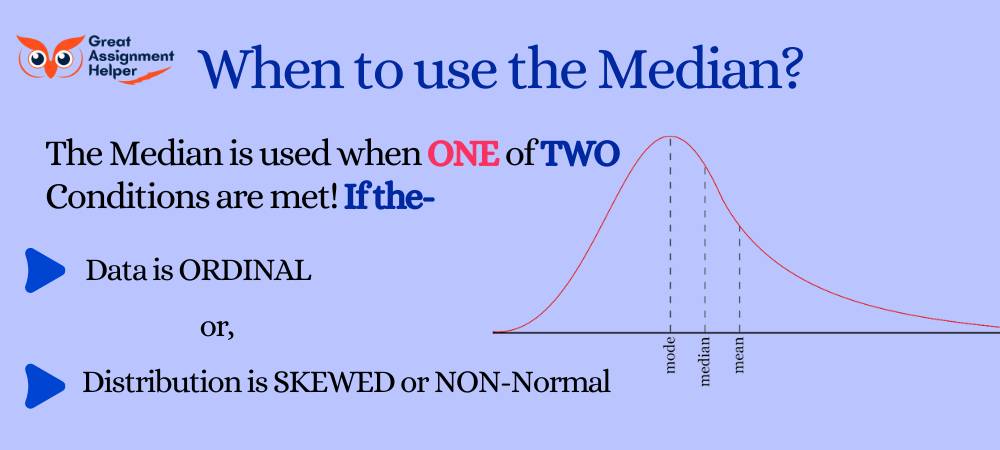
The median is a powerful measure of central tendency, particularly useful in specific scenarios where other measures like the mean might not provide the most accurate reflection of the data's central point. Here are key situations when opting for the median is advantageous:

1. Skewed Distributions: In datasets where values are not symmetrically distributed, leading to skewness, the median offers a more reliable central value. It is not influenced by extreme outliers, which can significantly affect the mean.
2. Outliers Present: When your dataset includes outliers or extremely high or low values, the median provides a better sense of the typical value. Unlike the mean, it remains unaffected by these extremes.
3. Ordinal Data: For datasets consisting of ordinal data (ranked categories), the median can indicate the middle ranking more effectively than the mean, which may not be applicable to non-numerical data.
4. Non-Normal Distributions: In distributions that are not normal or have unknown distributions, the median can serve as a safer bet for identifying the central tendency, as it doesn't assume any specific distribution shape.
5. Income and Property Values: For economic data like income or property values, which often have a skewed distribution, the median gives a clearer picture of what is typical, avoiding the distortion that high-value outliers can cause.
6. Comparative Analysis: When comparing central tendencies across different datasets, especially those with different sizes or distributions, the median can provide a consistent and comparable measure.

Choosing the median as your measure of central tendency under these circumstances ensures a more accurate and meaningful representation of your dataset, especially in analyses where understanding the middle value is crucial.

Wrapping Up

In conclusion, mastering the concept of the median is essential for anyone tackling statistics assignments or dealing with data analysis. It's a robust measure that offers clarity and insight, especially in datasets where the mean might be misleading due to outliers or skewness. For students and professionals seeking statistics assignment help, platforms like Great Assignment Helper emerge as invaluable resources. Offering comprehensive online assignment help, they provide the guidance and support needed to navigate the complexities of statistical analysis. Whether it's understanding the median or any other statistical concept, turning to such platforms can make a significant difference in achieving academic and professional success.

Read More Blogs: Proving 2+2 = 5: A Mathematical Journey